Здравствуйте!
Посоветуйте пожалуйста что да как. Сначала определения и постановка, а потом будет вопрос.
Определения.Пусть

линейное пространство. Назовём
ядром 
произвольного множества

совокупность таких его точек

, что для каждого

найдётся такое число

, что

при

. Выпуклое множество ядро которого не пусто, называется
выпуклым телом.
Пусть

линейное пространство. Множество

называется симметричным, если из

следует

.
Пусть

линейное пространство. Назовём

- семейство всех выпуклых симметричных подмножеств пространства

совпадающих со своим ядром.
Пусть

топологическое линейное пространство (далее ТЛП). Оно называется локально выпуклым, если в нём всякое непустое открытое множество содержит непустое выпуклое открытое подмножество
Постановка.Доказать, что семейство

является определяющим семейством окрестностей нуля для некоторой локально выпуклой отделимой топологии в пространстве

. (Эта топология называется
ядерно-выпуклой)
Замечание.Все определения из Колмогорова Фомина и задача тоже оттуда. В седьмом издании на странице 183. Также замечу, что определение
локально выпуклой отделимой топологии я не нашёл в учебнике, но подозреваю, что под ним понимается следующее: если в линейном пространстве введена такая топология, то оно становиться 1) ТЛП 2) Локально выпуклым ТЛП 3)Выполняется третья(по классификации К.Ф.) аксиома отделимости, т.е. точка и не содержащее её замкнутое множество имеют непересекающиеся окрестности. При попытке доказательства я использовал такую трактовку этого определения и, не отрицаю, что она заведомо может быть ошибочна.
Первые шаги в доказательстве.Пусть задано линейное пространство

. Рассмотрим свойства семейства

. Рассмотрим произвольное множество

. В силу выпуклости и симметричности можно записать:

. Значит любое множество из семейства

содержит 0. Далее несложные рассуждения приводят к тому, что произвольное объединение множеств из семейства

является симметричным множеством. Пусть

. Рассмотрим их пересечение. Если

, то

и
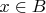
, но так как

- симметричные, то и

и

, это означает, что

. Получаем, что

также симметричное множество. Я думаю, но могу конечно ошибаться, что эту логику можно провести с произвольным набором множеств из семейства

и получить, что пересечение произвольного числа множеств из

есть симметричное множество. Также известно,что пересечение произвольного числа выпуклых множеств есть выпуклое множество. Что делать с ядром такого произвольного пересечения - не знаю. Итак полученные свойства семейства

в произвольном линейном пространстве

:
1) Произвольное объединение множеств из этого семейства есть симметричное множество.
2) Произвольное пересечение множеств из этого семейства есть выпуклое? симметричное множество.
Далее. Пусть в

введена некоторая ядерно-выпуклая топология. Заметим, что если пространство

является локально выпуклым, то для любой точки

и любой её окрестности

найдётся такая выпуклая окрестность

, что

. Нас интересует это свойство для

. Из написанного следует, что в любой окрестности нуля есть выпуклая окрестность нуля. Это означает, что определяющую систему окрестностей нуля в нашем случае можно задать как систему всех выпуклых окрестностей нуля. Назовём её

.
Далее, как мне кажется, надо рассмотреть в каких соотношениях находятся семейства

и

при заданной ядерно-выпуклой топологии. А именно:
1)Показать, что семейство

есть семейство открытых множеств.
2) В любую выпуклую окрестность нуля можно засунуть множество из семейства

Тогда получиться,что в любой окрестности нуля есть множество из семейства

, это множество содержит ноль, и является открытым - значит оно также является окрестностью нуля. Требуемое утверждение.
Загвоздка в том что пункт 1) и 2) у меня не получается доказать.
Спасибо за то, что прочитали до конца. На вот эту
http://dxdy.ru/topic24354.html просьба сразу не отсылать - читал, но не помогло. Пишу в ТЕХе не часто - возможны опечатки.