Помогите разобраться с определением групп

[Keter]

Определение. Непустое множество $\mathbb {G}$ называется группой, если выполнено четыре условия:
1) Закон композиции. Каждой паре элементов $a, b \in \mathbb {G}$ сопоставляется третий элемент этого же множества, называемый произведением элементов и обозначаемый $ab$. Закон композиции называется также бинарной операцией.
2) Закон ассоциативности. Для любых трех элементов $a, b, c \in \mathbb {G}$ имеет место равенство $(ab)c = a(bc)$.
3) В $\mathbb {G}$ существует левая единица $e$: $ea = a, \forall a \in \mathbb {G}$.
4) Для каждого элемента $a \in \mathbb {G}$ существует по крайней мере один левый обратный элемент $a^{-1} \in \mathbb {G}$: $a^{-1} a = e$.
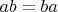
Множество элементов с одной бинарной операцией, которая удовлетворяет только условию ассоциативности, называется полугруппой. Полугруппа с единичным элементом называется моноидом. Если для любых двух элементов $ab = ba$, то группа (или полугруппа) называется коммутативной или абелевой. В противном случае группа (или полугруппа) называется неабелевой.

Пример 2.2.1. Пусть $n \mathbb {Z}$ – множество целых чисел, делящихся на $n$, где $n$ – произвольное натуральное число. Это множество содержит число $0$ при всех $n$, и в нем определены операции сложения $(+)$ и умножения $(\cdot)$. Относительно этих операций пара $(n \mathbb {Z}, +)$ является коммутативным моноидом, где роль единицы выполняет число $0$, а пара $(n \mathbb {Z}, \cdot)$ – коммутативной полугруппой без единицы, если $n ≥ 2$.

Помогите разобраться, почему в примере у пары $(n \mathbb {Z}, +)$, роль единицы выполняет именно число $0$? Почему ноль?

[erwins]

$0+a=a$

[Keter]

Спасибо. Уже понял, что операция сложения происходит.