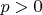Точные квадраты. (Лёгкая разминка.)

[hippie]

а) В десятичной записи числа первая цифра единица, а все остальные — четвёрки. При каком количестве четвёрок это число — точный квадрат? (Указать все возможные ответы и доказать, что других не существует.)

б) В десятичной записи числа последняя цифра пятёрка, а все остальные — двойки. При каком количестве двоек это число — точный квадрат? (Указать все возможные ответы и доказать, что других не существует.)

[Shadow]

а) Кроме 14 все делятся на 4, получается $n^2=3611\hdots 1$ Квадрат не может заканчивать на 11, так что проверяем 36 - подходит, 361 подходит. Т.е $144, 1444$
б) Аналогично делим на 25, потом умножаем на 9, получаем $(3n)^2=800\hdots 01$
$\\(2k+1)^2=8\cdot 10^m+1\\ k(k+1)=2^{m+1}\cdot 5^m$

Влево произведение двух последовательных чисел, одно из них нечетное, т.е равно $5^m$, другое $2^{m+1}$
$\\5^m-2^{m+1}=\pm 1\\ m_1=0, m_2=1$

Решения $25, 225$

-- 24.02.2012, 16:11 --

Вообще то одно может быть $5^{m-p}$, другое $5^p\cdot 2^{m+1}$, но тогда их разность не будет 1 (будет делится на 5) при $p>0$