Задано симплектическое многообразие

Имеется гамильтонова система с гладким гамильтонианом

. Рассмотрим уровень энергии

1) Доказать, что всякое гладкое многообразие

трансверсальное к векторному полю гамильтоновой системы с гамильтонианом

является симплектическим относительно
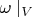
.
2) Предположим определено еще одно многообразие

трансверсальное к векторному полю гамильтоновой системы с гамильтонианом

. Доказать, что если c помощью фазового потока
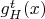
каждому

поставлена в соответствие точка

, то полученное отображение

-- каноническое. Здесь через

обозначено минимальное время при котором

.