Всё чётко с этими рядами, да не совсем. По теореме Лорана разлагаю всю жизнь, сейчас не получается. Есть функция

, в области

разложил, а вот в области
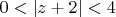
, не могу. Как я понимаю, функция в этом круге не аналитична, туда особая точка

, попадает, как быть?