Вы хотите честно это сделать? А то есть такой читерский трюк: если
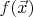
— непрерывная в

функция, то

задает открытую область: раз

непрерывна, то

тоже непрерывны, и каждая из них сохраняет знак в некоторой окрестности...

Если честно — представьте этот конус. Рассеките его плоскостью

, в этой плоскости постройте маленькую окружность с центром в

, дополните ее до шара — ну и все.