Аналитическая геометрия: треугольник

[yourredvenus]

В треугольнике угол при вершине $B$ 60 градусов
Из этой вершины проведены медиана
$x+11/19=y-5/-7=z+10/16$
и высота
$7x-9y-7z-32=0$
$14x+4y-7z-62=0$
Площадь треуголтника $S=54\sqrt{3}$
Найти коорд. вершин тр-ка
Подскажите как найти A и С?

[RIP]

Я решал так:
Во-первых, я так понял, что уравнение медианы такое

$$\frac{x+11}{19}=\frac{y-5}{-7}=\frac{z+10}{16}$$

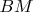
Я записал уравнения медианы и высоты в параметрическом виде, после чего легко найти угол между ними. Задача по сути свелась к планиметрической: В $\Delta ABC$ известны угол $\angle ABC=\frac{\pi}3$, угол между медианой $BM$ и высотой $BH$ и площадь $S_{\Delta ABC}=54\sqrt3$. Что надо найти, я уточню ниже. Удобно ввести систему координат с центром в точке $M$ и осью абсцисс, направленной вдоль стороны $AC$. Тогда координаты вершин треугольника будут $A(-a;0),\ B(x,y),\ C(a,0)$. Можно считать, что $x>0,\ y>0$. Условия $\angle ABC=\frac{\pi}3$ и $\angle MBH=\ldots$ дают 2 уравнения на $x,y$ ($a$ я рассматриваю как параметр), которые легко решаются. После этого из условия $S_{\Delta ABC}=54\sqrt3$ легко находится $a$. Дальше можно решать по-разному. Я делал так: нашел длины $BM,\ BH$ и выразил вектора $\overrightarrow{BA},\ \overrightarrow{BC}$ через $\overrightarrow{BM},\ \overrightarrow{BH}$. Зная это и параметрические уравнения медианы и высоты, а также координаты точки B, легко найти координаты 2 других вершин. Очевидно, что задача имеет 2 решения (решения, в которых $A$ и $C$ меняются местами, я считаю за одно решение).
P.S. Числа подобраны так, что координаты вершин - целые числа.