Кубик бросают

раз.
Какова вероятность получить неубывающую последовательность?
Первые 4 значения посчитала "вручную":

Как найти производящую функцию?
Как вообще решать подобный класс задач?
(готовность думать имеется)
...
Вот...пока писала...и переводила дЫхалку...там получается каждый раз умножить на 3 и отнять 9. Но это интуитивная догадка, а существует ли какой-бы-то-ни-было общий метод для таких задач?
P. S. Вообще, очень тесты на
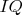
напоминает...