Дана последовательность подмножеств

множества

. Нужно доказать, что последовательность сходится тогда и только тогда, когда последовательность характеристических функций
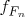
множеств

сходится к

.
Начал с необходимости. Пусть сходится, тогда

. А тут непонятно, что значит предел последовательности функций

.