Есть простое соображение. (Это не совсем строгое доказательство, но близко к нему.)
Поскольку замедление пропорционально скорости, то результат не зависит от того в каких единицах измеряется скорость.
Т.е. если вначале скорость равна 20уес (условных единиц скорости), то через полминуты скорость будет равна 10уес.
Вначале уес=1узел;
через полминуты уес=
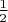
узла;
ещё через полминуты (т.е. через минуту после начала движения) уес=

узла;
ещё через полминуты (т.е. через полторы минуты после начала движения) уес=

узла.
Таким образом, в конце второй минуты скорость будет равна

узла.
PS Интереснее используя только это рассуждение (И НИКАКИХ ДИФФУРОВ!) найти скорость лодки через 45 секунд после отключения мотора.