Кстати, о КТО — она верна для случая, когда мы рассматриваем бесконечное число идеалов?
Насчет того, что
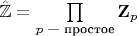
— как это доказывает, что

? Если мое вложение — не эпиморфизм, то должен же быть элемент в

без прообраза в

, можно ли его как-то явно выписать (хоть один)?
-- Чт янв 26, 2012 23:16:15 --Дело в том, что существует доказательство изоморфности. Верное или нет — не знаю, лично я его не видел.