Игрок проигрывает при любой игре. Заметим, что игрок не может бесконечно долго "оставаться на одном и том же аргументе", т.к. тогда значение каждой следующей функции на этом аргументе должно быть меньше предыдущего, а все эти значения - натуральные числа. Значит аргумент должен увеличиваться до бесконечности, причём на каждом аргументе происходит только конечное количество уменьшений функции. Для каждого аргумента, нас интересуют только две крайние функции - "вход" с меньшего аргумента и "выход" на больший аргумент. Т.е., не ограничивая общности, можно считать, что есть возрастающая последовательность аргументов

и последовательность функций

из

, такая, что

и нужно доказать, что такая последовательность не может быть бесконечной ни при какой игре игрока. Идея состоит в том, чтобы параллельно с "многочленами"

рассматривать приведённые "многочлены", в которых коэффициенты всегда меньше текущего аргумента, но которые, в отличие от исходных "многочленов", будут обязательно убывать в соответствии с некоторым определённым на

порядком, превращающим его во вполне упорядоченное множество. Т.к. в этой последовательности найдётся наименьший элемент, то он же будет в ней и последним, т.е. сама последовательность на нём обрывается и обязана быть конечной.
Более строго это выглядит так. Пусть

- множество неотрицательных целых чисел. Определим рекурсивно следующие множества с заданным на каждом из них линейным порядком:
1)

- множество состоит из единственного элемента, являющегося пустым множеством. Будем также обозначать этот элемент знаком

.
2) Для любого

, если

вместе с порядком

определены для всех

, то определим

как множество конечных упорядоченных наборов

При этом

соответствует пустой набор, т.е.

также включается в

. Для любых элементов

, если

,

и различие в этих последовательностях начинается с

-го элемента, то порядок между

и

определяется таким же, как и между

и

; в случае отсутствия

-го элемента в наборе, задающем один из элементов, он (элемент) считается меньшим. В частности,

- наименьший элемент

. Для определённости стоит отметить, что элемент, определяемый набором из одного элемента
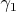
при

- это не то же самое, что этот элемент сам по себе, так же, как и
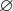
не то же самое, что

. В частности,

можно считать по сути дела эквивалентом

и в нём, наряду с

, будет присутствовать также элемент

, соответствующий единице в

.
По индукции доказывается, что:
1)

;
2) Порядок на каждом следующем множестве совпадает с порядком на предыдущем;
3) Порядок на каждом множестве является полным.
После этого можно естественным образом определить упорядоченное множество

которое будет вполне упорядоченным.
Теперь каждому элементу из

можно поставить в соответствие некоторую функцию

, также рекурсивным образом:
1) Элементу

из

ставится в соответствие функция

.
2) Для любого

, если каждому

уже поставлена в соответствие некоторая функция

, то для любого

положим

.
По индукции доказывается, что при таком сопоставлении каждому элементу из

в

будет сопоставлена та же функция, что и в

.
Если
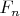
- множество функций, соответствующих всем элементам из
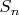
, а

- множество функций, соответствующих всем элементам из

, то тогда можно показать, что

есть множество

, фигурирующее в условии задачи.
Для любого натурального

также определим множество

аналогично

, но с той разницей, что на каждом шаге в определении

будем требовать, чтобы ни один элемент

не входил в набор, задающий определяемый в

элемент,

(или больше) раз. Очевидно,

и

.
Можно определить операцию "увеличения на единицу"

так: если

,

, то

определяется как набор (опять же из
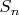
), задаваемый дописыванием

справа к набору, определяющему

. Очевидно, тогда для любого

и для любого натурального

:

. Кроме этого, приведением к общему шагу определения
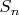
легко доказать, что

.
Утверждение 1. Если  ,
,  и
и  , то
, то  .
.Можно доказать индукцией по шагу построения

при каждом фиксированном

, с использованием вышеуказанных свойств "прибавления единицы" и определения функции

, постепенно производя свёртку "хвоста" последовательности, задающей

, начиная с самого меньшего элемента.
Утверждение 2. Если  , то для любого
, то для любого  существует такой элемент
существует такой элемент  , что:
, что:
а)  ;
;
б)  ;
;
в)  при всех
при всех  .
.Доказывается также индукцией по шагу построения

при каждом фиксированном

. Если

, то либо какой-то элемент

не принадлежит

и мы заменяем его на

, найденный для

и существующий в силу индуктивного предположения, либо какой-то элемент

встречается в последовательности (минимум)

раз и тогда мы выбрасываем эту группу из

элементов (оставляя остальные вхождения

, если они есть) и заменяем её на единственный элемент

. Полученный ряд, упорядоченный соответствующим образом, и определит

. При определении

, возможно, придётся повысить шаг

, но это не нарушит логики индукции, ибо мы использовали доказываемое утверждение только для

(и то только в первом случае).
Взяв какой-либо исходный элемент

и многократно применяя утверждение 2, получим некоторую последовательность

элементов

, такую, что для любого

а)

;
б)

;
в)

при всех

.
В силу свойства a), эта последовательность не может быть бесконечной и мы рано или поздно придём к элементу из

. Поэтому, в силу свойств б) и в), верно
Утверждение 3. Если  ,
,  , то найдётся такой элемент
, то найдётся такой элемент  , что:
, что:
а)  ;
;
б)  при всех
при всех  .
.Возвращаясь к задаче, будем считать, не ограничивая общности, что

. По каждой функции

,

, построим элемент

вместе с соответствующей функцией

, следующим образом. Как было сказано выше,

, поэтому

для некоторого

. Если

, то полагаем

, иначе используем утверждение 3 и положим

, найденному из этого утверждения. В любом случае,

, а

. Учитывая, что

, при любом

получим:

Но

и

, поэтому из

и из утверждения 1 получаем, что

. Значит последовательность

- убывающая во вполне упорядоченном множестве

а, стало быть, конечна.

Доказанное утверждение есть обобщение
теоремы Гудстейна, которую, как известно, невозможно доказать, исходя только из аксиом Пеано. "Игра", которая фигурирует в теореме Гудстейна, ограничена тем, что там обязано чередоваться увеличение аргумента ровно на единицу с уменьшением значения функции тоже ровно на единицу, причём коэффициенты у всех частей вновь выбираемой функции должны быть меньше текущего аргумента, т.е. там "игра" по сути дела детерминирована и состоит только из выбора начального значения. Здесь же, благодаря автору задачи, появилось некоторое разнообразие.