Можно доказать индукцией по

, что для любого натурального

такое верно, т.е.

- где

и

- произведения факториалов простых чисел.
1)

.
2) Пусть теперь утверждение доказано для всех

, где

- натуральное, большее 1. Докажем его для

.
Если

- составное число, то

, где

и

- натуральные числа, меньшие

. Для

и

утверждение уже доказано,

и

, поэтому
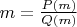
, где

,

.
Если

- простое число, то

, значит и
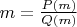
, где

,

.