Я приведу пример,когда при одинаковой плотности , меньшая масса движется медленне большей
вот он
есть ось на оси закреплены перпендикулярно оси бесконечное количество отрезков
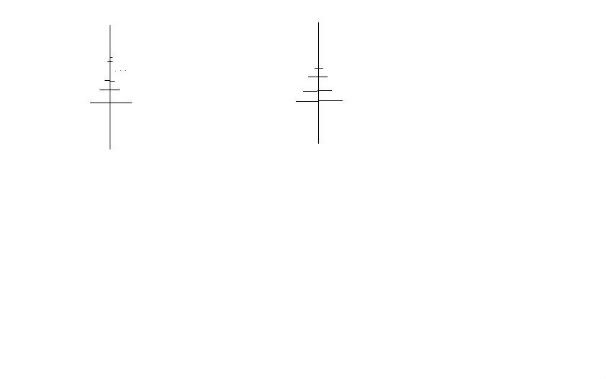
первая система отрезков:
масса всех отрезков образует последовательность

длина тоже

плотность равна

прилагаем некое усилие ,и получаем кинетическую энергию из формулы T=

-момент инерции,

-скорость центра масс i-того стержня(=0)
находим угловую скорость w
и суммарная скорость всех точек всех отрезков -

(<бесконечности))
вторая система
масса =

длина =

плотность та же (

)скорость -

(<бесконечности)
n выбираем так,чтобы суммарная скорость первой системы была меньше второй
усили одинаковое , так что... и как такое объяснить?