Пусть

- любые индексы одной чётности и

- номер наибольшей цифры в двоичном разложении, различной у

и

, т.е.

. Тогда

и между
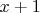
и

включительно есть ровно одно число, делящееся на

, а именно

. Рассмотрим равенство

Разделим любой из сомножителей

в левой части на максимальную степень двойки, содержащуюся в нём; то же самое сделаем и с соответствующим ему множителем в правой части, учитывая, что если

, где

нечётное (а

только для

и меньше

для остальных
![$d \in (x,y]$ $d \in (x,y]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91caef1f268e6f4890033baefe8afb2f82.png)
), то

. Допустим теперь, что

и

дают одинаковые остатки при делении на
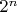
. Тогда они дают и одинаковые остатки, обозначим их

, при делении на

. Рассмотрим (1), полученное после вышеуказанного деления на степени двойки, по модулю

. Как было сказано выше, каждому множителю

в левой части будет соответствовать

в правой, причём для всех множителей, кроме одного, будет

, откуда

и

. (1) перепишется так:

Т.к.

и

одной чётности, то

нечётно (если не включать частные для

в ряд

). Обозначив

, получаем:


и

-нечётные числа, поэтому из последнего сравнения следует такое:

Но последнее невозможно. Полученное противоречие доказывает различие остатков от деления

и

на
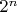
, соответствующих

и

одинаковой чётности. Различие же для

и

разной чётности следует из того, что

при чётных

и

при нечётных

- это можно получить, рассматривая (1) для

по модулю

.