На частицу массой

действует сила

, где

и

- положительные постоянные. При
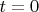
скорость частицы

. Найти работу силы за очень большой промежуток времени (

)
Рассуждения :
1. Работа переменной силы определяется

2. Границы интегрирования из условия о времени ясны, но вот непонятно что использовать заместо

, поэтому пока так:

Подскажите пожалуйста, как применить данную формулу для решения задачи.
P.S. Не принимайте близко к сердцу, возможно написал много глупостей.