Дан интеграл

и поверхность
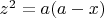
внутри цилиндра
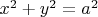
, нужно найти поверхностный интеграл 1-го рода. Для этого я выразил
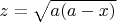
, нашел

, перешел к двойному интегралу по проекции на плоскость

, проекция-окружность радиуса

. Получился такой интеграл
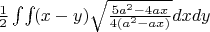
. Правильно ли я сделал? Я не знаю как извлечь этот интеграл.