Разбиение шахматной доски на прямоугольники

[Ktina]

Шахматная доска разбита на N непересекающихся прямоугольников (по линиям сетки). В каждом прямоугольнике белых и чёрных клеток поровну. Площади прямоугольников попарно различны.

а) Найти наибольшее возможное значение N.

б) Сколькими способами это можно сделать при наибольшем N?
(два способа считаются за один, если у них одно и то же множество значений площадей прямоугольников разбиения, и различными в противном случае)

[Dave]

Выпишем площади прямоугольников, получающихся при разбиении, в порядке возрастания: $S_1<S_2<\ldots<S_N$. Из того, что в каждом прямоугольнике белых и чёрных клеток поровну, следует, что все эти числа чётны. Из того, что прямоугольники разбивают шахматную доску, следует, что сумма их площадей равна площади шахматной доски, т.е. $S_1+S_2+\ldots+S_N=64$. Пусть $a_1=\frac {S_1} 2 - 1$, $a_i=\frac {S_{i}-S_{i-1}} 2 - 1$, $i=2,3,\ldots,N$. Тогда все $a_i$ - целые неотрицательные числа и $S_i= 2\left(i+ \sum\limits_{k=1}^i a_k\right)$, $i=1,2,\ldots,N$, а сумма $S_i$ выражается так:

$$\sum\limits_{i=1}^N S_i =2 \sum\limits_{i=1}^N \left(i+ \sum\limits_{k=1}^i a_k\right)=2 \sum\limits_{i=1}^N i + 2 \sum\limits_{1 \leqslant k \leqslant i \leqslant N} a_k = N(N+1) + 2 \sum\limits_{k=1}^N \sum\limits_{i=k}^N a_k =$$ $$=N(N+1) + 2 \sum\limits_{k=1}^N (N-k+1)a_k.$$

Значит $Na_1+(N-1)a_2+\ldots+a_N = 32 - \frac {N(N+1)} 2$. Отсюда следует, что при $N \geqslant 8$ разбиений быть не может. При $N=7$ сумма $Na_1+(N-1)a_2+\ldots+a_N$ должна принимать значение $4$, чему соответствуют такие пять наборов $a_i$: $\{0,0,0,1,0,0,0\}$, $\{0,0,0,0,1,0,1\}$, $\{0,0,0,0,0,2,0\}$, $\{0,0,0,0,0,1,2\}$, $\{0,0,0,0,0,0,4\}$, которым соответствуют такие наборы $S_i$: $\{2,4,6,10,12,14,16\}$, $\{2,4,6,8,12,14,18\}$, $\{2,4,6,8,10,16,18\}$, $\{2,4,6,8,10,14,20\}$, $\{2,4,6,8,10,12,22\}$ Последний набор нереализуем, ибо площадь $22$ может соответствовать только прямоугольнику $2 \times 11$, 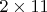который невозможно "втиснуть" в шахматную доску по линиям сетки. Первые же четыре набора реализуемы, например, так:

$\begin{bmatrix} 6 & 4 & 2 & 10 & 10 & 10 & 10 & 10\\ 6 & 4 & 2 & 10 & 10 & 10 & 10 & 10\\ 6 & 4 & 12 & 12 & 12 & 12 & 12 & 12\\ 6 & 4 & 12 & 12 & 12 & 12 & 12 & 12\\ 6 & 14 & 14 & 14 & 14 & 14 & 14 & 14\\ 6 & 14 & 14 & 14 & 14 & 14 & 14 & 14\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ \end{bmatrix}$ $\begin{bmatrix} 2 & 2 & 6 & 6 & 4 & 4 & 4 & 4\\ 14 & 14 & 6 & 6 & 8 & 8 & 8 & 8\\ 14 & 14 & 6 & 6 & 8 & 8 & 8 & 8\\ 14 & 14 & 12 & 12 & 12 & 12 & 12 & 12\\ 14 & 14 & 12 & 12 & 12 & 12 & 12 & 12\\ 14 & 14 & 18 & 18 & 18 & 18 & 18 & 18\\ 14 & 14 & 18 & 18 & 18 & 18 & 18 & 18\\ 14 & 14 & 18 & 18 & 18 & 18 & 18 & 18\\ \end{bmatrix}$

$\begin{bmatrix} 6 & 6 & 2 & 2 & 4 & 4 & 4 & 4\\ 6 & 6 & 8 & 8 & 16 & 16 & 16 & 16\\ 6 & 6 & 8 & 8 & 16 & 16 & 16 & 16\\ 10 & 10 & 8 & 8 & 16 & 16 & 16 & 16\\ 10 & 10 & 8 & 8 & 16 & 16 & 16 & 16\\ 10 & 10 & 18 & 18 & 18 & 18 & 18 & 18\\ 10 & 10 & 18 & 18 & 18 & 18 & 18 & 18\\ 10 & 10 & 18 & 18 & 18 & 18 & 18 & 18\\ \end{bmatrix}$ $\begin{bmatrix} 2 & 2 & 8 & 4 & 4 & 6 & 6 & 6\\ 14 & 14 & 8 & 4 & 4 & 6 & 6 & 6\\ 14 & 14 & 8 & 10 & 10 & 10 & 10 & 10\\ 14 & 14 & 8 & 10 & 10 & 10 & 10 & 10\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ \end{bmatrix}$

При этом, поскольку у каждого прямоугольника в любом разбиении есть чётная сторона, то, очевидно, чёрных и белых клеток в нём будет поровну.
Ответ: a) 7; б) 4 способами.

[Ktina]

Dave в сообщении #522604 писал(а):

$\begin{bmatrix} 6 & 4 & 2 & 10 & 10 & 10 & 10 & 10\\ 6 & 4 & 2 & 10 & 10 & 10 & 10 & 10\\ 6 & 4 & 12 & 12 & 12 & 12 & 12 & 12\\ 6 & 4 & 12 & 12 & 12 & 12 & 12 & 12\\ 6 & 14 & 14 & 14 & 14 & 14 & 14 & 14\\ 6 & 14 & 14 & 14 & 14 & 14 & 14 & 14\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ \end{bmatrix}$ $\begin{bmatrix} 2 & 2 & 6 & 6 & 4 & 4 & 4 & 4\\ 14 & 14 & 6 & 6 & 8 & 8 & 8 & 8\\ 14 & 14 & 6 & 6 & 8 & 8 & 8 & 8\\ 14 & 14 & 12 & 12 & 12 & 12 & 12 & 12\\ 14 & 14 & 12 & 12 & 12 & 12 & 12 & 12\\ 14 & 14 & 18 & 18 & 18 & 18 & 18 & 18\\ 14 & 14 & 18 & 18 & 18 & 18 & 18 & 18\\ 14 & 14 & 18 & 18 & 18 & 18 & 18 & 18\\ \end{bmatrix}$

$\begin{bmatrix} 6 & 6 & 2 & 2 & 4 & 4 & 4 & 4\\ 6 & 6 & 8 & 8 & 16 & 16 & 16 & 16\\ 6 & 6 & 8 & 8 & 16 & 16 & 16 & 16\\ 10 & 10 & 8 & 8 & 16 & 16 & 16 & 16\\ 10 & 10 & 8 & 8 & 16 & 16 & 16 & 16\\ 10 & 10 & 18 & 18 & 18 & 18 & 18 & 18\\ 10 & 10 & 18 & 18 & 18 & 18 & 18 & 18\\ 10 & 10 & 18 & 18 & 18 & 18 & 18 & 18\\ \end{bmatrix}$ $\begin{bmatrix} 2 & 2 & 8 & 4 & 4 & 6 & 6 & 6\\ 14 & 14 & 8 & 4 & 4 & 6 & 6 & 6\\ 14 & 14 & 8 & 10 & 10 & 10 & 10 & 10\\ 14 & 14 & 8 & 10 & 10 & 10 & 10 & 10\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ 14 & 14 & 8 & 20 & 20 & 20 & 20 & 20\\ \end{bmatrix}$

При этом, поскольку у каждого прямоугольника в любом разбиении есть чётная сторона, то, очевидно, чёрных и белых клеток в нём будет поровну.
Ответ: a) 7; б) 4 способами.

У меня тоже вышло 7 и 4, только разбиение вот такое получилось:

$\begin{bmatrix} 20 & 20 & 20 & 20 & 20 & 10 & 10 & 8\\ 20 & 20 & 20 & 20 & 20 & 10 & 10 & 8\\ 20 & 20 & 20 & 20 & 20 & 10 & 10 & 8\\ 20 & 20 & 20 & 20 & 20 & 10 & 10 & 8\\ 2 & 4 & 4 & 4 & 4 & 10 & 10 & 8\\ 2 & 6 & 6 & 6 & 6 & 6 & 6 & 8\\ 14 & 14 & 14 & 14 & 14 & 14 & 14 & 8\\ 14 & 14 & 14 & 14 & 14 & 14 & 14 & 8\\ \end{bmatrix}$ $\begin{bmatrix} 18 & 18 & 18 & 18 & 18 & 18 & 2 & 2\\ 18 & 18 & 18 & 18 & 18 & 18 & 10 & 10\\ 18 & 18 & 18 & 18 & 18 & 18 & 10 & 10\\ 6 & 6 & 6 & 6 & 6 & 6 & 10 & 10\\ 8 & 8 & 8 & 8 & 4 & 4 & 10 & 10\\ 8 & 8 & 8 & 8 & 4 & 4 & 10 & 10\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ \end{bmatrix}$

$\begin{bmatrix} 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ 16 & 16 & 16 & 16 & 16 & 16 & 16 & 16\\ 14 & 14 & 14 & 14 & 14 & 14 & 14 & 6\\ 14 & 14 & 14 & 14 & 14 & 14 & 14 & 6\\ 12 & 12 & 12 & 12 & 12 & 12 & 4 & 6\\ 12 & 12 & 12 & 12 & 12 & 12 & 4 & 6\\ 10 & 10 & 10 & 10 & 10 & 2 & 4 & 6\\ 10 & 10 & 10 & 10 & 10 & 2 & 4 & 6\\ \end{bmatrix}$ $\begin{bmatrix} 18 & 18 & 18 & 18 & 18 & 18 & 6 & 8\\ 18 & 18 & 18 & 18 & 18 & 18 & 6 & 8\\ 18 & 18 & 18 & 18 & 18 & 18 & 6 & 8\\ 12 & 12 & 12 & 12 & 4 & 4 & 6 & 8\\ 12 & 12 & 12 & 12 & 4 & 4 & 6 & 8\\ 12 & 12 & 12 & 12 & 2 & 2 & 6 & 8\\ 14 & 14 & 14 & 14 & 14 & 14 & 14 & 8\\ 14 & 14 & 14 & 14 & 14 & 14 & 14 & 8\\ \end{bmatrix}$