Сообщения, передаваемые по каналу связи, составляются из 3 знаков - A, B, C. Из-за помех каждый знак принимается правильно с вероятностью 0,6 и принимается ошибочно за любой из двух других с вероятностью 0,2. Для увеличения вероятности правильного приёма, каждый знак передаётся 5 раз.
За переданный знак принимается знак, который чаще всего встречается в принятой пятёрке знаков. Если наиболее частых знаков два, то из них выбирается равновероятно один.
Используя полиномиальную схему, найти вероятность правильного приёма знака при указанном способе передачи.
-- 24.12.2011, 14:24 --Для начала решил описать множество возможных событий при передачи знаков:

- принято 5 верных знаков

- принято 4 верных и один ошибочный
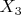
- принято 3 верных и 2 ошибочных
-- 24.12.2011, 14:28 --Вероятность этих событий нахожу по формуле Бернулли:

, где

,
 -- 24.12.2011, 14:33 --
-- 24.12.2011, 14:33 --Далее необходимо рассмотреть событие, когда наиболее часто встречающихся знака два:

- принято 2 верных знака, 2 ошибочный одного типа и 1 ошибочный другого.
В такой ситуации Бернулли не работает...