Доктор говорит "резать" - резать!

[Ktina]

(Оффтоп)

Анек в качестве преамбулы:
Рабинович получает на почтамте телеграмму: "доктор говорит резать резать". И тут же отправляет ответную: "доктор говорит резать резать".
Рабиновича вызывают в КГБ, будучи уверенными в том, что поймали агента Моссада. Но всё оказалось проще. Родственник Рабиновича спрашивал в телеграмме: "Доктор говорит "резать" - резать?". А Рабинович ему ответил: "Доктор говорит "резать" - резать!"

Какой наименьший квадрат можно разрезать на 9 прямоугольников, среди которых нет двух конгруэнтных?
(все прямоугольники должны иметь только целочисленные стороны, параллельные сторонам квадрата)

[svv]

Отвечу Вам вопросом на вопрос: а какую наименьшую площадь могут иметь $9$ неконгруэнтных прямоугольников? (Ktina, Вы помните, для меня слова "попарно" не существует)

Всё очень просто. Берём все прямоугольники площади $1$, потом все площади $2$ и т.д., пока их не наберётся $9$ штук. Очевидно, их суммарная площадь неуменьшаема. Прямоугольники эти:
$1\times 1,\; 1\times 2,\; 1\times 3,\; 1\times 4,\; 2\times 2,\; 1\times 5,\; 1\times 6,\; 2\times 3,\; 1\times 7$
Их суммарная площадь равна $38$. Но она не есть полный квадрат. Значит, придётся взять прямоугольники большей площади. Следующий полный квадрат $49$. Если повезёт, он и будет ответом -- но не меньший.

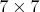
И, действительно, $7\times 7$ уже можно замостить (более спокойный термин, чем "разрезать"), например, так:
$1$ строка -- $1\times 7$
$2$ строка -- $1\times 6$ и $1\times 1$
$3$ строка -- $1\times 5$ и $1\times 2$
$4$ строка -- $1\times 4$ и $1\times 3$
Оставшийся прямоугольник $3 \times 7$ уж как-нибудь на два не использовавшихся ранее прямоугольника разобъём.