Оценить дисперсию ошибки оценки

[urankhai]

Добрый день!
Помогите, пожалуйста, найти правильную оценку дисперсии ошибки оценки. У самого как то не получается довести до конца решение этой задачи.

Ставится стандартная задача МНК
$f_i(t)=c_i(t) X + r_i(t), \quad i =1,.., N$
данное выражение переписываем в векторном виде
$z(t) = b(t) X + r(t) $, где $z(t), b(t), r(t)$ векторы составленные соответственно из $f_i(t), c_i(t), r_i(t)$.

В данной задаче принимаем, что процессы $r_i, \, i=1,..,N$ являются "цветными" шумоми. С помощью преобразования Фурье выбелим шумы, получим следующее выражение:
$Z(\omega) = B(\omega) X + R(\omega). $ Здесь для прямого преобразования я использую следующую формулу $F(\omega) = \frac{1}{2\pi}\int f(t) e^{-i\omega t} dt. $
Теперь, пользуясь утверждением об оптимальной оценке (откуда уже не помню), говорим что оценка $X$ находится из уравнения
$ \left\{\int \limits_{-\infty}^{+\infty} B^*(\omega)\Gamma (\omega) B(\omega) d\omega \right\} X= \int\limits_{-\infty}^{+\infty} B^*(\omega) \Gamma (\omega) Z(\omega) \, d\omega.$
Здесь $\Gamma (\omega) =[S_r(\omega)]^{-1}$. Дисперсия ошибки $X$ имеет вид
$D_{XX}^{-1}=\int \limits_{-\infty}^{+\infty} B^*(\omega)\Gamma (\omega) B(\omega) d\omega$.
Теперь переходим непосредственно к поиску оценки дисперсии. На этом шаге считаем, что процессы $c_n$ - это куски стационарных случайных процессов $\xi_n$ со спектральными плотностями $S_n(\omega)$, то есть:
$c_{n}(t)= \left\{ \begin{array}{ll} \xi_n(t), &t\in[-T,T] \\ 0, &t\in(-\infty, -T]\cup[T, +\infty) \end{array} \right.$
Спектральное представление процесса $c_n(t)$ имеет вид
$C_n(\omega)=\int\limits_{-\infty}^{+\infty} \frac{\displaystyle \sin T(\omega-\nu)}{\displaystyle \pi (\omega-\nu)} \, d V_n(\nu)$.
Для процесса $b(t)$ спектральное представление будет следующим
$B(\omega)= \int\limits_{-\infty}^{+\infty} \frac{\displaystyle \sin T(\omega-\nu)}{\displaystyle \pi (\omega-\nu)} \, d W(\nu).$
$W(\nu)$ - матричный процесс, строки которого - процессы $V_n(\nu)$. Будем считать, что $V_n(\nu)$ - независимы и имеют интенсивности $S_n(\nu)$.
Подставляя это разложение в выражения для дисперсии, получим
$D_{XX}^{-1} = \int\limits_{-\infty}^{+\infty} d\omega \int\limits_{-\infty}^{+\infty} \int\limits_{-\infty}^{+\infty} \frac{\displaystyle \sin T(\omega-\nu) \sin T(\omega-\sigma)} {\displaystyle \pi^2 (\omega-\nu)(\omega-\sigma)} \, dW^*(\sigma) \Gamma (\omega) \, dW(\nu).$

Вот с этого места у меня начинаются всякого рода фокусы. Нахожу матожидание от этого выражения
$M[D^{-1}_{XX}]=\int\limits_{-\infty}^{+\infty} d\omega \int\limits_{-\infty}^{+\infty} \sum\limits_{n=1}^N \left[\Gamma_{nn}(\sigma) S_n(\sigma)\right] \frac{\displaystyle \sin^2 T(\omega-\sigma)}{\displaystyle \pi^2 (\omega-\sigma)^2} \, d\sigma,\quad \Gamma_{nn}$ - диагональные элементы матрицы $\Gamma(\omega)$. Вроде бы ошибок нет в этом месте. Теперь устремляя $T\rightarrow \infty$ и пользуясь свойством 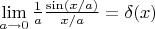$\lim\limits_{a\rightarrow 0} \frac{1}{a}\frac{\sin(x/a)}{x/a} = \delta(x)$ источник получим следующее выражение для матожидания дисперсии
$M[D^{-1}_{XX}] = \frac{1}{ \pi^2} \int\limits_{-\infty}^{+\infty} \sum\limits_{n=1}^N \left[\Gamma_{nn}(\omega) S_n(\omega)\right] \, d\omega.$ В этом результате не совсем уверен. На этом месте я хочу сказать, что сама дисперсия при $T\rightarrow \infty$ равна математическому ожиданию.
То есть
$ D^{-1}_{XX} = \frac{1}{ \pi^2} \int\limits_{-\infty}^{+\infty} \sum\limits_{n=1}^N \left[\Gamma_{nn}(\omega) S_n(\omega)\right] \, d\omega.$
Как можно строго доказать последнее утверждение?

[urankhai]

urankhai в сообщении #517108 писал(а):

Теперь устремляя $T\rightarrow \infty$ и пользуясь свойством $\lim\limits_{a\rightarrow 0} \frac{1}{a}\frac{\sin(x/a)}{x/a} = \delta(x)$ источник получим следующее выражение для матожидания дисперсии
$M[D^{-1}_{XX}] = \frac{1}{ \pi^2} \int\limits_{-\infty}^{+\infty} \sum\limits_{n=1}^N \left[\Gamma_{nn}(\omega) S_n(\omega)\right] \, d\omega.$

Здесь не совсем правильно посчитал. У меня получилось два возможных ответа:
1. $M[D^{-1}_{XX}] = \int\limits_{-\infty}^{+\infty} \sum\limits_{n=1}^N \left[\Gamma_{nn}(\omega) S_n(\omega)\right] \, d\omega,$
либо
2. $M[D^{-1}_{XX}] = \frac{T}{ \pi} \int\limits_{-\infty}^{+\infty} \sum\limits_{n=1}^N \left[\Gamma_{nn}(\omega) S_n(\omega)\right] \, d\omega.$

В первом случае считаю, что \lim\limits_{T\rightarrow \infty}\frac{\sin^2 T(\omega-\sigma)}{\pi^2 (\omega-\sigma)^2} = \lim\limits_{T\rightarrow \infty}T^2\cdot\frac{\sin^2 T(\omega-\sigma)}{T^2\pi^2 (\omega-\sigma)^2} = \delta^2(\omega-\sigma),

во втором случае, \lim\limits_{T\rightarrow \infty}T\cdot\frac{\sin T(\omega-\sigma)}{T\pi (\omega-\sigma)} \cdot\frac{\sin T(\omega-\sigma)}{\pi (\omega-\sigma)} = \delta(\omega-\sigma)\cdot\lim\limits_{T\rightarrow \infty}\frac{\sin T(\omega-\sigma)}{\pi (\omega-\sigma)}.

Объясните пожалуйста, где я ошибаюсь?