Здравствуйте,помогите разобраться
Независ случ. величины e и n подчинены показательным законам распределения
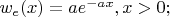

,y>0:$
нужно записать выражение для совместной ПВ и ФР системы случ величин e и n.а также найти вероятность совместного выполнения условий e<5 и n<4
с совместной ФР распределения я вроде как разобрался т.к. случ величины независ. я просто взял двойной интеграл от их произведения
с ПВ вообще не уверен,взял частные производные от ФР
как быть с последним заданием ума не приложу
подскажите пожалуйста)