Степенной ряд (область сходимости), предел

[lampard]

ewert в сообщении #514336 писал(а):

lampard в сообщении #514332 писал(а):

$|x-1|<3$

Неверно.

Кроме того, не забывайте (это уже в дальнейшем): признак Даламбера даёт достаточное условие сходимости, но формально ничего ровным счётом не говорит о расходимости.

А как же не дает? Если предел $\lim\limits_{n\to \infty}\dfrac{|a_{n+1}|}{|a_n|}>1$ -- то расходится ряд или что-то я путаю? Или вы имеете ввиду, что признак ничего не говорит при $\lim\limits_{n\to \infty}\dfrac{|a_{n+1}|}{|a_n|}=1$ ?

$\Big|\dfrac{3}{1-x}\Big|<1$

$\dfrac{3}{|1-x|}<1$

Домножим на $|1-x|$ обе части

$|1-x|>3$

$|x-1|>1$

$x\in(-\infty,-2)\cup(4,\infty)$ --- интервал сходимости

При $x=-2$ ряд расходится по предельному признаку сравнения с гармоническим рядом.

При $x=4$ ряд сходится по признаку Лейбница

$x\in(-\infty,-2)\cup[4,\infty)$ -- область сходимости.

А радиуса -- нет. Теперь правильно?

[ewert]

lampard в сообщении #514341 писал(а):

А как же не дает? Если предел $\lim\limits_{n\to \infty}\dfrac{|a_{n+1}|}{|a_n|}>1$ -- то расходится ряд или что-то я путаю?

Расходится, но не по признаку Даламбера.

Лучше (раз уж тема -- "степенные ряды"), чтоб не путаться, сделайте замену $z=\frac1{1-x}$. Для переменной $z$ получится уже воистину степенной ряд; вот честно, по шаблону и найдите область сходимости для новой переменной. А потом формально пересчитайте эту область на старую переменную.

-- Вс дек 11, 2011 18:50:32 --

lampard в сообщении #514341 писал(а):

При $x=-2$ ряд расходится по предельному признаку сравнения с гармоническим рядом.

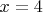
При $x=4$ ряд сходится по признаку Лейбница

$x\in(-\infty,-2)\cup[4,\infty)$ -- область сходимости.

Теперь правильно. Однако про внутренний интервал по-прежнему формально так ничего и не сказано.

[lampard]

Понятно, спасибо!