Утверждения, связанные с функц-ми последовательностями.

[Peek-A-Boo]

Помогите пожалуйста доказать следующие утверждения:
1. Если $f(x)$ непрерывна на всей числовой оси, то последовательность $f_n(x)=\sum_{k=0}^{n-1}{\frac{1}{n}f(x+\frac{k}{n})}$ сходится равномерно на любом конечном отрезке [a,b]. 2. Если $f(x)$ бесконечно дифференцируема на всей числовой оси, а последовательность $f^{(n)}(x)$ сходится равномерно к $g(x)$ на каждом конечном интервале (a,b), то $g(x)=ce^x$, где c - константа.

По первому номеру: данная последовательность является последовательностью интегральных сумм функции f(k) на интервале от x до x+1, которая сходится к соответствующему интегралу. Но не получается придумать, как доказать равномерность сходимости.
По второму номеру никаких идей нет.

[ewert]

Peek-A-Boo в сообщении #512657 писал(а):

которая сходится к соответствующему интегралу. Но не получается придумать, как доказать равномерность сходимости.

В непрерывном случае сходимость интегральной суммы к интегралу оценивается через модуль непрерывности (который участвует в определении равномерной непрерывности). А непрерывная функция равномерно непрерывна на любом конечном промежутке, в т.ч. и захватывающем любой промежуток интегрирования.

-- Ср дек 07, 2011 22:39:25 --

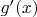
Насчёт второго. Если $f_n(x)\equiv f^{(n)}(x)$, то из равномерной сходимости $f_n(x)$ к $g(x)$ и, соответственно, равномерной сходимости $f_n'(x)=f^{(n+1)}(x)$ хоть к чему-то (а значит, к $g'(x)$) следует $g'(x)\equiv g(x)$. Далее -- теория дифуравнений, иначе как-то совсем бессознательно.

[Peek-A-Boo]

Со вторым спасибо. А вот с модулем непрерывности не совсем понятно: если модуль непрерывности - функция, ставящая каждому дельта в соответствие эпсилон (где для любых $x_1$ и $x_2$, таких, что $|x_1-x_2|<\delta $, $|f(x_1)-f(x_2)|<\varepsilon$), то как она связана со сходимостью интегральной суммы и ее остаточным членом?

[ewert]

Peek-A-Boo в сообщении #512834 писал(а):

как она связана со сходимостью интегральной суммы и ее остаточным членом?

Тривиально связана: погрешность для любой интегральной суммы не превосходит по по абсолютной величине умноженного на длину промежутка интегрирования значения модуля непрерывности для данного ранга дробления.