Задачи на многообразия.

[3.14]

Здравствуйте.
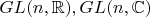
1)Доказать, что группы $GL(n,\mathbb{R}), GL(n,\mathbb{C})$ являются гладкими многообразиями.
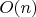
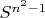
2)Доказать, что $O(n)}$ лежит на сфере $S^{n^2 - 1}$ радиуса $\sqrt n$.
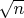
3)Привести пример многообразия с двумя несогласованными гладкими структурами.

Вот я попробовал :
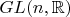
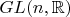
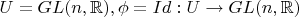
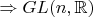
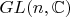
1)Введем структуру гладких многообразий на $GL(n,\mathbb{R})$. Т к $GL(n,\mathbb{R})$ - открытое, то у нас одна карта $U = GL(n,\mathbb{R}), \phi = Id : U \rightarrow GL(n,\mathbb{R})$ - гомеоморфизм $\Rightarrow GL(n,\mathbb{R})$ - гладкое многообразие.Для $GL(n,\mathbb{C})$ аналогично. Я не уверен, что решение верное.
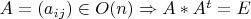
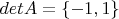
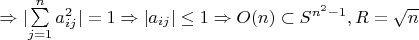
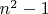
2)Пусть $A = (a_{ij}) \in O(n) \Rightarrow A*A^t = E$ и $detA = \lbrace -1, 1 \rbrace$. Возьмем детерминант по модулю $\Rightarrow \lvert \sum\limits_{j = 1}^{n} a_{ij}^2 \rvert = 1 \Rightarrow \lvert a_{ij} \rvert \leq 1 \Rightarrow {O(n) \subset S^{n^2 -1}, R = \sqrt n $. Про радиус понятно, что корень из $n$, а вот я не показал, почему степень у сферы $n^2 - 1$..из чего это видно?
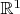
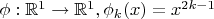
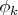
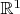
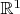
3)Вот рассмотрим на $\mathbb{R}^1$ отображение $\phi : \mathbb{R}^1 \to \mathbb{R}^1, \phi_k(x) = x^{2k - 1}$, где $k$ - целое положительное число. Как показать, что $\phi_k$ задает карту на $\mathbb{R}^1$ с областью определения, совпадающей со всей прямой $\mathbb{R}^1$. Тогда эти атласы попарно не согласованы?