Матрицы

[Евгеша]

Пусть есть матрица $A$. Как найти матрицу $B$ такую, что $AB = 0$? ($A$ и $B$, разумеется, ненулевые.)

[ИСН]

Для начала: что надо потребовать от матрицы A?

[Joker_vD]

Решить систему уравнений, чего ж тут еще сделать?

[Евгеша]

ИСН
А что, не для любой матрицы найдется матрица, обнуляющая ее?

Joker_vD
Ниче се так системка получится

[ИСН]

Ну, найдите для такой: $\left(\begin{matrix}1&0\\ 0&1\end{matrix}\right)$

[Евгеша]

ИСН
Ну да, единичная не в счет. А остальные?

[JMH]

Как не в счёт, а $\left(\begin{matrix}0&1\\ 1&0\end{matrix}\right)$??

-- Пн ноя 28, 2011 13:16:34 --

Запишите Ваше матричное уравнение в виде системы уравнений воспользовавшись определением произведения матриц - сразу появятся идеи :)

[Joker_vD]

Евгеша
А вы чего хотели? Считайте-считайте. Между прочим, такая вот задача встречается в теории кодирования, когда по порождающей матрице $G$ кода надо найти его проверочную матрицу $H$ (или наоборот) — эти матрицы связаны условием $GH^T=0$.

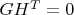
Вообще говоря, матрица $B$ находится довольно неоднозначно — в ней может быть полным-полно л.з. столбцов. Что же насчет матрицы $A$ — там есть определенное уловие на ранг.

[venco]

Евгеша в сообщении #509385 писал(а):

А что, не для любой матрицы найдется матрица, обнуляющая ее?

Если у матрицы $A$ есть обратная, то $B=A^{-1}AB=A^{-1}0=0$.
Значит у $A$ не должно быть обратной матрицы.