Формирование линейной системы уравнений и ее решение

[ildgin]

есть формула 15,1 расписав которую должна получиться система уравнений из 9 строк и 9 -ю неизвестными, вкратце i и j изменяются от 1 до 3, решается граничная задача для которой половина из t и U известны это может быть известны t и необходимо найти U или известна часть того и другого, остальные переменный все находятся и решаются, я столкнулся с тем что получается матрица у которой много нулевых элементов

мне кажется что я неправильно суммирую по индексам, может кто нибудь сталкивался с такого вида формулами и может подсказать что за чем идет
заранее спасибо

[zhe]

Не могли бы вы немного разъяснить суть проблемы пока что я понял только что вы получаете сильно разряженную матрицу для Метода Грнаничных Элементов. Но на сколько я знаю в данном методе матрицы всегда получаются сильно разряженными. Если матрица не совсем нулевая и ее детерминант не ноль то в чем собственно проблема?

[ildgin]

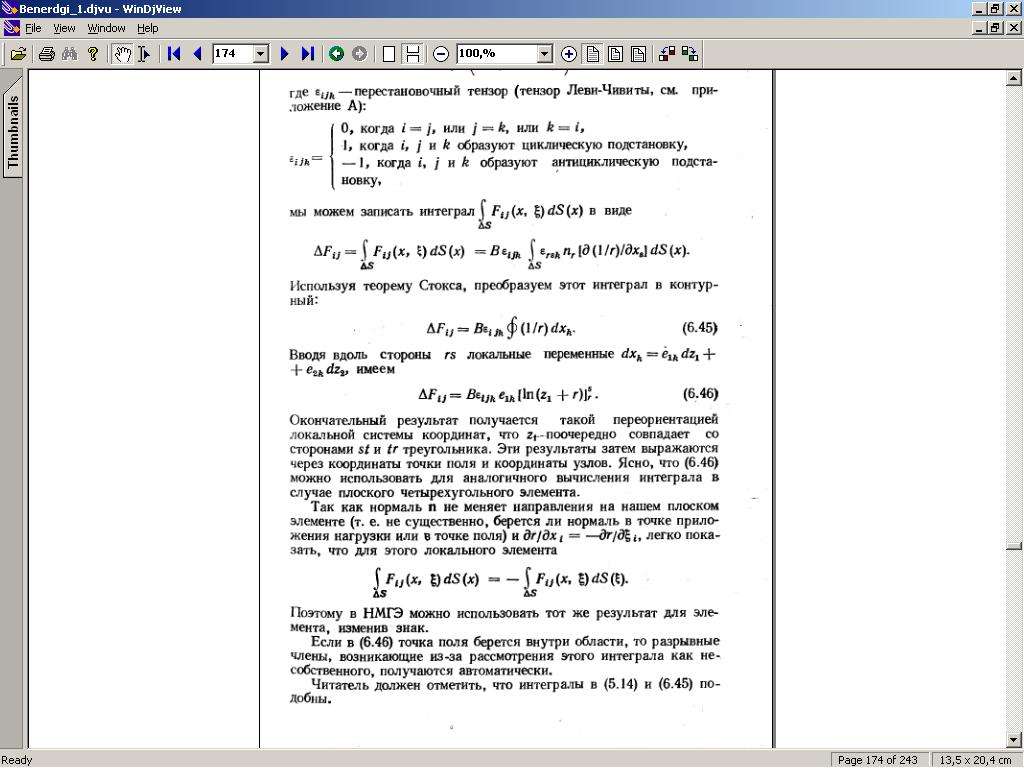
у меня получается система уравнений которую я свожу к матричному виду и при попытке решить ее методом Гаусса или методом вращений не находит решения, мне кажется что я неправильно веду суммирование элементов по индексам, дело в том что переменные Gij и Fij в интегралах содержат символ Кронекера и тензор перестановок Леви-Чивиты из-за которых у меня в матрице столбцы 1, 5 и 9 нулевые и при таком раскраде матрица вырожденая получается, не могли бы вы написать как бы вы проводили суммирование матрицы и расписали это интрегральное уравнение повторюсь что все неизвестные находятся интересует только развертка уравения в виде линейной системы уравнений, также проверял в маткаде левую и правую часть уравнения 15,1 левая дает строки уравнения а именно переменная Cij а в правой части tki или Uki дает столбцы, а вот в каком порядке перебирать индексы не совсем ясно так как они повторяются и похоже должны быть разными

может поможет описание входящих в формулу 15,1 переменных, нехватает только Nk но с ним нет каких либо затруднений это переменная характеризующая геометрию граничных элементов

[ildgin]

может кто то из вас имеет свои соображения по тому как эта формула расписывается в систему линеных уравнений а то все варианты которые я перебрал дают вырожденную систему уравнений, мне поможет какое либо предположение что бы было над чем подумать

[ildgin]

с системой уравнений разобрался, никто не сталкивался с проблемой нехватки памяти при решении системы уравнений порядка 100тыс строк со столькими же неизвестными, предлагают сжимать ее, но дело в том что матрица разреженная но не диагональная, т.е. есть нулевые элементы их довольно то много но расположены как попало, нет закономерности, из-за этого не могу посчитать свою задачу точнее

и есть ли наиболее подходящий метод решения таких систем, пока пользуюсь методом ортогонализации с минимизацией невязки, пробовал метод вращений ищет слишком долго решение по сравнению с вышеописанным