Всё правильно, подходят числа вида

, где

— такое нечётное простое, что

— составное. Очевидно, таковых бесконечно много
Да, действительно.
Вот моё решение:
Все степени семёрки (кроме первой) подходят. Действительно, p может быть только 7, но тогда q-r - тоже степень семёрки, а значит даёт остаток 1 при делении на 6. Число (большее 1), дающее остаток 1 при делении на 6, не может быть разностью двух простых, так как одно из этих простых должно быть 2, а другое 3.
Также несложно доказать, что подходят все нечётные степени пятёрки, кроме первой. Док-во аналогично.
Вот попробуйте теперь
второй пункт решить. Я его тоже не осилил, а Ксюша смогла.
-- 25.11.2011, 13:19 --Все числа типа

, где

- простые число вида
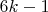
. Можно ли утверждать, что их кол-во бесконечно?
Только не "минус", а "плюс".
Но это тупиковый путь, ведь придётся доказывать бесконечность множества простых вида

.