Вы не имели права, работая с четырьмя векторами изотропного базиса приплетать по сути пятый вектор из совершенно другого, уже неизотропного базиса. Проделайте все построения в изотропном базисе и все должно встать на свои места. Или лучше вообще забыть про изотропный базис и все проделывать в "ортонормированном". В последнем "нормальная" мнимая единица

вполне законна и составляет часть этого базиса.
Я всегда в вычислениях стараюсь пользоваться обозначением

, где

,

--- комплексные числа. Например,

.

--- это не базисный элемент, а координата элемента двумерного векторного пространства над

. Я на этом не настаиваю, просто поясняю свои обозначения, которые являются в некотором смысле стандартными (и от которых я зря один или два раза отошел).
-- 26.04.2012, 01:03 --Выше Вы говорили, что меняя базис, можно при фиксированном четырехмерном замкнутом контуре переходить от формул типа (26-27) к (28-29). Теперь выходит, что для получения формул типа (28-29) нужен не просто переход к новому базису, а принципиально изменить ТИП контура. В моем понимании так оно и есть.
Если я так говорил, то я Вас обманывал.
И для этого действительно нужно от обычного замкнутого контура перейти к контуру с элементами гиперболичности.
Чем они необычные? Это обычные замкнутые несамопересекающиеся контуры в
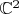
. Я же не виноват, что не все они друг другу гомотопны, а теорему надо доказывать для всех.
То, что Вы добиваетесь этого некими манипуляциями со значениями

и

говорит лишь о том, что Вы неявно в финслеровом четырехмерии кардинальным образом сменили режим обхода этого пространства, сделав из контура евклидова типа псевдоевклидов тип. Ну, или наоборот.
Еще раз. Есть задача доказать некоторые факт про замкнутые контуры в
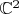
. Мы знаем, что для гомотопных контуров ответы одинаковые. Очевидно, что ответ скорее всего зависит от гомотопического класса контура. Поэтому естественным вопросом является классифицировать все контуры. Это легко.
У Вас вот вообще в статье теорема заявляется для произвольного контура, а доказывается только для типов (1,1), (1,-1), (1,0) и (0,1). А на самом деле еще есть много неэквивалентных им контуров, и для них будет другой вид формулы Коши.