Минимальная площадь треугольника

[acme]

Помогите, пожалуйста, решить задачу:
Найти минимально возможную площадь равностороннего треугольника со стороной $6\sqrt[]{3}$.

[ИСН]

Минимально возможную? Их что, много разных?

[acme]

ИСН в сообщении #505286 писал(а):

Минимально возможную? Их что, много разных?

Но просят же, не просто площадь треугольника найти, а минимально возможную. Что это значит?

[zhoraster]

Значит, что хотят запутать. Пишите смело единственно возможную площадь (она же, кстати, будет и минимальной).

[acme]

Задача имеет следующее условие:
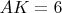
$ AD $ - биссектриса треугольника $ \Delta ABC $. На продолжении прямой $ AD $ за точку $A$ взята точка $K$ такая, что $ AK = 6 $ и $ \angle BKC = 60^o = \angle BAD = \angle CAD $. Найти минимально возможную площадь треугольника $ \Delta BKC $.
У меня получился $ \Delta BKC $ - равносторонний, со стороной $ 6\sqrt3 $. Его площадь $ S = 27\sqrt3 $, а как найти его минимально возможную площадь?

[ИСН]

Читать условие - это очень, очень полезно.

-- Пт, 2011-11-18, 23:12 --

Теперь давайте вместе понимать смысл букв. Что Вы делали? Откуда пришла информация, что BKC - равносторонний? Старшина этого вроде не говорил.

[zhoraster]

(Оффтоп)

А ответ $27\sqrt{3}$ ВНЕЗАПНО правильный.