Решение в общем виде дифура второго порядка.

[AC-130U Spectre]

Ay+By''+C=0
Решение на WolframAlpha можно найти, но мне нужен ход решения.
И, если можно, объясните пожалуйста каждый шаг как полному идиоту.

[Утундрий]

Почему "как"?

[ewert]

(Оффтоп)

Утундрий в сообщении #496534 писал(а):

Почему "как"?

Жостко, но справедливо.

AC-130U Spectre, тут не учебник. Тут не излагаются темы. Тут разъясняются лишь конкретные вопросы.

[AC-130U Spectre]

Жаль.

[Toucan]

Утундрий в сообщении #496534 писал(а):

Почему "как"?

Утундрий, убедительная просьба: постарайтесь, пожалуйста, воздерживаться от подобных оскорбительных комментариев, не имеющих отношения к существу заданного вопроса.

[AC-130U Spectre]

Кажется понял прикол, простите. Когда решал Ay+By'+C=0, там можно было просто перенести dy в одну сторону, dx в другую, и получалась экспонента с некими коэффициентами. Ay+By''=0 тоже легко:
$Ay=-B\cdot(d^2y/dx^2)$
$-Adx^2/B=(d^2y)/y$
$\int \int -Adx^2/B=-A/B$
$\int \int (d^2y)/y$ не знаю.
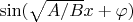
Видимо должно получиться $\sin(\sqrt{A/B}x+\varphi)$. Я проверил, так и есть.
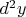
Однако не могу понять смысл символа $d^2y$. Как его интегрировать то? В чём отличие от $dx^2$ ?
Ну и когда вводится независимая константа, то решить задачу перенося дифференциалы и переменные в разные стороны я не могу.

[ewert]

AC-130U Spectre в сообщении #496695 писал(а):

Однако не могу понять смысл символа $d^2y$. Как его интегрировать то?

А никак.

AC-130U Spectre в сообщении #496695 писал(а):

В чём отличие от $dx^2$ ?

Лучше спросите, что у них общего: ни по тому, ни по другому интегрировать нельзя. Можно интегрировать лишь по обычному дифференциалу; у Вас же в первом случае -- второй дифференциал, а во втором -- и вообще квадрат дифференциала (а вовсе не дифференциал квадрата).

Возьмите книжку и почитайте раздел "понижение порядка дифференциальных уравнений". Или "линейные уравнения с постоянными коэффициентами".