Что можно сказать в общем случае о решениях (или хотя бы о конечности числа решений) для соотношения вида

, где

- произвольные целые константы (с условием целочисленности

),

- переменная. Кроме малой теоремы Ферма, бесконечности числа чисел Кармайкла и

я больше ничего не знаю (т.е. случай
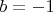
довольно хорошо изучен + немного о случае

). Хотелось бы знать при каких

соотношение имеет бесконечное число решений, при каких - конечное.
(по мотивам)
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=440782