Приветствую.
Эта задача, в общем-то, несколько надуманная, по своей природе она из той же серии, что «полуночные задачи» Кэрролла. Но мне кажется занятной. Если найдём решение, её, наверное, можно будет в «Олимпиадные задачи» поместить :)
Рассмотрим уравнения вида

, где

,

— некоторая группа функций

относительно операции композиции,

— какое-нибудь множество. Функция

дана, функцию

надо найти. Есть какие-нибудь идеи, как решать такие уравнения?
Задача выше сформулирована в довольно общем виде, так что для иллюстрации приведу более частные примеры. Сначала пусть

,

— группа всех биекций

. Ясно, что в такой

всего два элемента. Тогда исходное уравнение при

(единичное отображение) имеет два решения:

и

, где

,

. При

исходное уравнение не имеет решений.
Теперь пусть
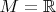
,

— группа всех функций

. Пусть

. Тогда решением исходного уравнения будет функция

. И, я думаю (правда, не уверен), это решение будет единственным.
Т.о., в принципе, обсуждаемое уравнение может либо не иметь решений вообще, либо иметь единственное решение, либо иметь много решений. Вот ещё пример, который выглядит очень простым, но я его пока не осилил. Пусть опять
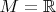
,

— какая-нибудь (какая угодно, лишь бы решение найти) группа функций

. И пусть

. Существует ли

, такая что


? Легко подобрать функцию

(где

— мнимая единица), но она не

. Есть какие-нибудь мысли, как решать хотя бы этот частный пример?