геометрическое место точек, заданных уравнением

[Legioner93]

Придется объяснять. Представьте, что вы нарисовали график окружности в координатах $Oxy$. Думаю, вы это умеете (если нет, то просто представьте окружность). А теперь вдруг добавляют вертикальную ось $Oz$ и просят построить график. Но ведь уравнение не изменилось! И в нём нет буквы $z$. Это значит, что про $z$ ничего не сказано - она может принимать любые значения. Т.е. 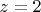на высоте $z=0$ лежит такая окружность, и на высоте $z=2$ на любой другой высоте $z$. Получается такая стопка окружностей (без дна и крышки). Представили? Большинство людей на вопрос о названии фигуры ответят, что это и есть цилиндр. Это цилиндр называется прямым круговым. Ну а теперь проделайте то же самое с вашей параболой.

[Dubarezova]

извените, но я с трудом представляю о чем идет речь. Не могли бы вы графически продемонстрировать мне окружность в пространстве

[ИСН]

Не могли бы. (Некоторые умеют, но это нарушение правил.) Шок трёхмерности каждый должен преодолеть самостоятельно.

[Dubarezova]

Спасибо, за столь красивое НЕТ!)))))

[ИСН]

Пожалуйста. А как Вы себе представляли положительный ответ?