Нужно определить область сходимости интеграла.

Замена

, тогда


.
Для первого интеграла

, тогда он сходится при

, т.е.

.
Для второго интеграла по признаку Дирихле
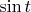
непрерывна и ограничена, а

сходится при

, т.е.

.
В конечном итоге получается

, но в ответе

.
Подскажите пожалуйста, где я неправ?