почему декартовы координаты не идентифицируют плоское двумерное Евклидово пространство ?
Попробую перевести: "Определяет ли двумерная Декартова система координат Евклидову плоскость"? Вы это хотели спросить?
Ответ: Да, определяет. Но слово "Декартова" существенно, т.е. базисные вектора в каждой точке этой СК должны быть единичны и ортогональны.
Мне сказали, что пространство не задается системой координат и они вообще слабо связаны.
Вероятно имелось в виду, что просто СК (без уточнения, что она Декартова) пространство не определит, не хватает
метрики - данных о том, каковы расстояния между точками, заданными соответствующими координатами.
Можно ли прямолинейную ортогональную СК задать в криволинейном пространстве той же размерности ?
Нет, нельзя. Только обращаю внимание, что цилиндр и конус не являются "криволинейными пространствами той же размерности", что и плоскость. На самом деле они имеют
нулевую кривизну, т.е. их можно развернуть (сохранив длины проведённых на них линий) в плоскость.
почему соответствующая этому пространству криволинейная СК не идентифицирует его
Аналогично координатам на плоскости, нужна метрика. Например, координаты "широты" и "долготы" на сфере -
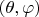
- следует дополнить информацией о расстояниях между точками сферы:

, где

- радиус сферы.
Можно ли криволинейную СК задать в плоском пространстве той же размерности ?
Пример криволинейных координат на плоскости - полярная СК.
Почему СК не обязана покрывать все точки пространства (или обязана) ?
А почему должна быть обязана?