Задача 55.12 из Кострыкина.
Пусть задано разложение подстановки

в произведение независимых циклов:

Найти разложение подстановки

в произведение независимых циклов.
Моё решение: рассмотрим некоторый цикл

. Покажем, что

. Действительно

, если

и
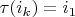
. В свою очередь

если

и

. То есть

(плюс краевой случай).
Отсюда заключаем, что

.
Это верно? Слишком просто получается, наверное, я что-то не учёл.