Ребята, помогите разобраться в задаче, условие ниже.
Из колоды 52 карты, вытаскивают 4 карты. Какова вероятность, что там будет хотя бы один туз.Считаю, что нужно действовать от обратного.

={Из 4 карт, хотя бы один туз}


={Из 4 карт, нет ни одного туза}

Сомнения у меня возникают на этапе, когда считаю вероятность того, что не будет тузов.

То есть первый раз есть 48 карт из 52, потом 47 из 52 и т.д.
Верно? Как правильно рассуждать в этой задаче.
-- 12.09.2011, 21:06 --Или нет, есть предположение, что

, объясните принцип рассуждений в таких задачах и нахождение
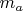
.