Bayes rule - какие меры и простраства?

[Bridgeport]

В книге Jun Shao есть такой пример:

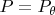
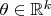
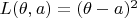
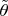
We usually try to find a Bayes rule or a minimax rule in a parametric problem where $P=P_{\theta}$ for a $\theta \in {\mathbb R^k}$. Consider the special case of $k=1$ and $L(\theta, a)=(\theta -a)^2$, the squared error loss. 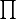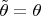Note that $r_T(\prod)=\int_{\mattbb R}E[\theta-T(X)]^2d\prod(\theta),$ which is equivalent to $E[{\tilde{ \theta}}-T(X)]^2$, where $\tilde{\theta}$ is a random variable having the distribution $\prod$ and, given $\tilde{\theta}=\theta$, the conditional distribution of $X$ is $P_{\theta}$. 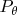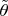Then, the problem can be viewed as a prediction problem for $\tilde{\theta}$ using functions of $X$. 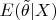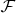Using previous results, the best predictor is $E(\tilde{\theta}|X)$, which is ${\cal F}$-Bayes rule w.r.t. 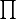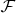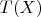$\prod$ with ${\cal F}$ being the class of rules $T(X)$ satisfying $E[T(X)]^2<\infty$ for any $\theta$

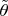
Мне не понятно выражение $E(\tilde{\theta}|X). \quad $ $\tilde{\theta}$ и $X$ находятся на разных пространствах с разными мерами. Подскажите!