Теория операторов. Открытость, замкнутость.

[Норберт]

Помогите найти простое доказательство следующего факта.

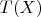
Пусть $X,Y$ - банаховы пространства и $T\in\mathcal{B}(X,Y)$. Если $T^*$ открыт, то $T(X)$ замкнуто.

Все доказательства, которые я нашел так или иначе сводятся к следующей "двойственной" теореме

Пусть $X,Y$ - банаховы пространства и $T\in\mathcal{B}(X,Y)$. Если $T^*$ инъективно и имеет замкнутый образ, то $T$ открыто.

Мне интересно, нет ли доказательства попроще без использования последней теоремы.

[Норберт]

Я придумал! Если кому интересно, то вот решение

Т.к. $T^*$ открыт, то существует $\varepsilon > 0$ такое что $B_{X^*}(0,\varepsilon)\subset T^*(B_{Y^*}(0,1))$. Тогда для любого $\psi\in X^{**}$ имеем

$$ ||T^{**}(\psi)||=||\psi\;\circ\; T^*||=\sup\{|(\psi\;\circ\; T^*)(g)| : g\in B_{Y^*}(0,1)\}=\sup\{|(\psi(T^*(g))| : g\in B_{Y^*}(0,1)\}\geq $$ $$ \sup\{|(\psi(f)| : f\in B_{X^*}(0,\varepsilon)\}\geq\varepsilon^{-1}\sup\{|(\psi(f)| : f\in B_{X^*}(0,1)\}=\varepsilon^{-1}||\psi|| $$

Пусть $i_X : X\to X^{**}$, $i_Y : Y\to Y^{**}$ - стандартные изометрические вложения во второе сопряженное, тогда для любого $x\in X$ имеем

$$ ||T(x)||=||i_Y(T(x))||=||T^{**}(i_X(x))||\geq\varepsilon^{-1}||i_X(x)||=\varepsilon^{-1}||x|| $$

Так как оператор T действует между банаховыми пространствами, то несложно показать, что полученное неравенство влечет замкнутость $T(X)$.