Пусть есть симметричная матрица 3 на 3 тогда ее полностью определяют 6 элементов этой матрицы можно ли эти 6 элементов выразить через меньшее число инвариантов матрицы ?
Любая матрица
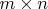
с вещественными коэффициентами, где
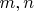
- натуральные числа, полностью задается одним вещественным числом. Действительно,

имеет мощность континуум, то есть существует биекция

. Таким образом, любая матрица

однозначно определяется числом

.
Если вы хотите более вменяемые инварианты, то придется обсудить, соответственно, конкретное и достаточно узкое значение термина "инвариант".