Назовём клетки соседними, если они находятся на одной вертикали либо на одной горизонтали.
Для начала избавимся от ладей. Поскольку всего у каждой клетки
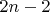
соседних, перефразируя условие, получаем, что для каждой пустой клетки число соседних пустых клеток не превышает

, и требуется доказать, что всего пустых клеток не более

.
Пусть на доске

пустых клеток. Для каждой пустой клетки найдём число соседних с ней, и получившиеся числа сложим. По условию, результат не должен превышать

. С другой стороны, тот же результат можно получить по-другому: сначала для каждой клетки найти число её соседей по вертикали, результаты сложить, затем повторить ту же операцию для горизонталей, результаты сложить, затем сложить две получившихся суммы. При этом если, допустим, на вертикали

пустых клеток, то при счёте по вертикалям каждая из них будет посчитана

раз, и, таким образом, эта вертикаль даёт вклад в общую сумму в размере

.
Нетрудно доказать, что сумма таких выражений по всем вертикалям достигает минимума, когда пустые клетки распределены по вертикалям максимально равномерно. Если забыть, что количество клеток на вертикали должно быть целым числом, мы получаем минимум

. Аналогично для горизонталей. Таким образом, получаем неравенство:

, или, после преобразований,
