Почему для линейных элементов выбираются точки коллокации - узлы. Для обусловленности матрицы? Граничные условия задаются также в узлах?
Я считаю, что так выбирают просто для удобства построения интерполирующих функций и сборки матрицы. Гораздо удобнее и для искомой функции, и для граничных условий задавать значения в одних и тех же узлах и использовать одинаковые интерполирующие функции.
Даже если точка коллокации находится не в узлах, но внутри элемента, то интеграл по этому элементу все-равно с особенностью. Диагональ в этом случае также должна быть довольно выраженной и с обусловленностью матрицы должно быть все хорошо. Вот если вынести точку коллокации за элемент, то тут да. Интеграл по элементу становится регулярным и обусловленность матрицы сильно ухудшается. Я тут попробовал рассмотреть три разные ситуации расположения узлов и точек коллокации.
Математическая постановка.Рассмотрим задачу Дирихле для уравнения Лапласа в замкнутой области

с достаточно гладкой границей



Требуется найти функцию

.Интегральное уравнение для решения этой задачи будет выглядеть так

где точки

,

-- фундаментальное решение уравнения Лапласа,

-- известная функция.
ДискретизацияСуть численного метода решения задачи заключается в дискретизации интегрального уравнения, т.е. замене непрерывного уравнения его дискретным аналогом. Для этого граница области разбивается на элементы, на элементах вводятся дискретные узлы, в этих узлах задаются некоторые значения -- коэффициенты, и непрерывная искомая функция

приближённо представляется в виде ряда по базисных функциям, умноженным на эти самые коэффициенты. Для того, чтобы получить систему линейных алгебраических уравнений необходимо, чтобы наше разложение выполнялось в ряде точек. Эти точки называются точками коллокации, а известные значения в этих точках обычно берутся из граничных условий.
Таким образом при дискретизации используются следующие понятия:
- элементы на которые разбивается граница, заданные своими вершинами;
- узлы;
- точки коллокации.
Существует несколько различных способов задания узлов и точек коллокации. Я тут попробую расписать три типичных случая, см. рис. 1.
Конфигурация AДанная конфигурация приведена на рис. 1A. Вершины элементов совпадают с узлами и точками коллокации. Базисные функции

линейны и непрерывны в вершинах элемента.
Задача 1. Приближённое представление функции.Требуется приближённо представить функцию

через её значения в узлах. Это удобнее всего делать отдельно для каждого элемента и в его локальных координатах.
Рассмотрим элемент

. Пусть значение искомой функции

в узле

равно

, а в узле

равно

. Так как мы строим линейную интерполяцию, то на элементе

функция должна представляться в виде:

В узле

значение

, а значение функции

, в узле

значение

, а значение функции

. В результате получаем следующую систему

откуда

Подставим найденные значения

и

в разложение функции

и сгруппируем относительно коэффициентов

и


Таким образом, мы получили приближенное представление функции, заданное через её значения в дискретных узлах,

, где


Первая задача решена.
Задача 2. Построить систему уравненийВ данной конфигурации точки коллокации совпадают с узлами. Рассмотрим точку коллокации

. Пусть известное значение функции в этой точке равно

. Интегральное уравнение для элемента

примет вид

В результате получим

Для остальных элементов

мы получаем аналогичные выражения. Интегралы в этих выражениях зависят только от геометрии.

это -- фундаментальное решение, зависящее от расстояния между точкой интегрирования

и точкой коллокации

.
Для элементов

, в которых точки

и

не совпадают, интегралы вычисляются численно. Для элемента

точки

и

совпадают при интегрировании и интеграл становится несобственным. Он обычно берется аналитически, и именно он усиливает диагональ. Благодаря этому интегралу обусловленность матрицы достаточно хорошая.
Матрица коэффициентов системы линейных алгебраических уравнений формируется из значений

, полученных путем вычисления данных интегралов для точек коллокации

и элементов, содержащих узел

. Так для точки

и элемента

получим


и сама матрица будет выглядеть так

Так как базисные функции

непрерывны на узлах, то среди интегралов на элементе

будет также интеграл с коэффициентом

. Его вычисленное значение нужно добавить к элементу матрицы

. Таким образом каждый элемент матрицы

состоит из суммы интегралов, вычисленных на смежных элементах, содержащих узел

.
Конфигурация BДанная конфигурация приведена на рис. 1B. Представление функции

остается таким же

Для получения значений коэффициентов матрицы системы линейных алгебраических уравнений нужно вычислить точно такие же интегралы


Единственное отличие заключается в том, что точка коллокации находится не в вершине элемента, а в его центре. Поэтому функция

будет другой и сам интеграл будет иметь другие значения. Но с обусловленностью матрицы должно быть все нормально, так как точка

все-равно находится на элементе и интеграл по этому элементу все-равно будет с особенностью. Но вот если вынести точку коллокации вообще за элемент, то интеграл становится регулярным, диагональ становится менее выраженной и матрица становится плохо обусловленной.
Так что на мой взгляд, такая конфигурация

ничем не хуже конфигурации

. Единственная проблема это -- как задавать в точке коллокации известное значение

. Если у нас граничные условия заданы аналитически, то проблем нет. А вот если они заданы численно, то гораздо естественнее все задавать именно в узлах.
Конфигурация CДанная конфигурация приведена на рис. 1C. В этой конфигурации узлы и точки коллокации вынесены внутрь элемента. Принципиальное отличие данной конфигурации от конфигураций

и

в том, что в вершинах элементов базисные функции получаются разрывными. Кроме этого число узлов в два раза больше, чем в конфигурациях

и

.
Построим интерполирующие функции. Пусть в локальных координатах узлы имеют следующие координаты

,

. Для построения интерполирующих функций рассмотрим следующую систему

откуда

Разложение функции

:

Таким образом, мы получили приближенное представление функции, заданное через её значения в дискретных узлах,

, где


Для получения значений коэффициентов матрицы системы линейных алгебраических уравнений нужно также вычислить интегралы от произведения интерполирующих функций на фундаментальное решение


Так как функции

разрывны в вершинах элементах, то, в отличие от конфигураций A и B, интегралы по элементу

не вносят вклад в значения
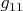
и

.
Такая конфигурация с разрывными элементами применяется на практике для того, чтобы учесть разрыв нормали в вершине элемента. Если решение с усреднением нормали в узле нас не устраивает по точности, то как раз и применяют такую разрывную конфигурацию.
И еще, возвращаясь к теме решателей. Используя lapack для матрицы 4800 на 4800, у меня получается решение порядка минуты. Хотя Mathematica решает секунд за 5-10... Может Mathematica считает ее как разреженную, поэтому скорость выше.
Мне кажется, что дело все-таки не в разреженности матрицы. Сам по себе LAPACK это -- наиболее классическая библиотека линейной алгебры, написанная на Фортране. Алгоритмы написаны таким образом, чтобы выполняться на любых машинах. Поэтому в них отсутствуют оптимизации под современные процессоры. Существуют специализированные библиотеки, который при сохранении
интерфейса LAPACK оптимизируют многие процедуры линейной алгебры с учетом особенностей современных процессоров (вычисления должны идти в кэше первого уровня, использовать SSE3, может быть разворачивать циклы). Таких библиотек я знаю две: MKL от Intel и свободная ATLAS. Если нужна максимальная производительность, то нужно использовать именно их.