новое решение сравнения 2^n = 3 (mod n)

[megamix62]

$4 700 063 497 = 19\cdot 47 \cdot 5263229$

притом

$2^{19\cdot47} \equiv 3\pmod{5263229}$
$2^{19} \equiv 3\pmod{47}$

$2^{19\cdot47\cdot 5263229} \equiv 3\pmod{4 700 063 497}$


причем все $n$ в найденных 5 сравнениях $2^n \equiv 3 (\mod n) $

равны $n\equiv 1 (\mod 6) $

[maxal]

maxal в сообщении #40078 писал(а):

А еще со мной связался Richard Guy, автор книги Unsolved Problems in Number theory, где эта задача значится под номером F10. В следующей редакции в ней будет упомянуто найденное решение.

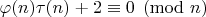
Решил другую задачку из UPINT - на этот раз B37, где упоминается сравнение Суббарао: $\varphi(n)\tau(n)+2\equiv 0\pmod{n}$, которому удовлетворяют все простые $n$, а среди составных до сегодняшнего дня было известно только $n=4$. Я нашёл новое составное решение:

$$n = 25643985470955911102 = 2 \cdot 61 \cdot 67 \cdot 6803 \cdot 29027 \cdot 15887233,$$

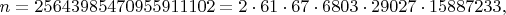
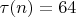
для которого $\tau(n)=64$ и сравнение приобретает вид равенства $64\varphi(n) + 2 = 31n$.

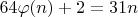
Жаль, что Ричарда Гая уже нет с нами, и новой редакции UPINT ждать не приходится.

PS. См. A389878