Задача по функциональному анализу

[petia.p]

$f_n(x)$ функциональный ряд
$ \chi_n(x)=\begin{cases} 1, |x-n|\leq\frac{1}{n^2}\\ 0, |x-n|>\frac{1}{n^2} \end{cases} $

$ f_n(x)=\begin{cases} (1-\chi_n(x))(x+\frac 1 n)^{-1}+n^\alpha\chi_n(x), x\geq1\\ 0, x<1 \end{cases} $

1) Каким значениям $\alpha$, у $f_n(x)$ существует поточечный предел и какая у него предельная функция?
2) Каким значениям $\alpha$, $f_n(x)$ равномерно сходится?
3) Каким значениям $\alpha$, $f_n(x)$ сходится по норме $L_2$ ?
4) Каким значениям $\alpha$, $f_n(x)$ сходится по норме $L_1$ ?

У меня получается что предельная функция:
$ f(x)=\begin{cases} \frac 1 x, 1\leq x<n-\frac{1}{n^2}, x>n+\frac{1}{n^2}\\ n^\alpha, n-\frac{1}{n^2}\leq x\leq n+\frac{1}{n^2}\\ 0, x<1 \end{cases} $
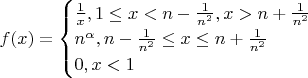
Вообще то в предельной функции не должен быть параметр $n$, но я не знаю как от него избавится.
Не знаю что делать.

[ewert]

У Вас просто гипербола $\dfrac{1}{x+{1\over n}}$, из которой выпирает одиночный прямоугольный пик, который с ростом номера удаляется вправо и уменьшается по ширине, а поведение его высоты как раз и зависит от альфы. Если бы пика не было, то со сходимостью (в каждом из смыслов) самой гиперболы всё было бы ясно. Остаётся выяснить, при каких альфах каждая из сходимостей не нарушается при добавлении пика. Тут тоже всё достаточно очевидно.