Рассмотрите прямое произведение множеств интегрирования по переменным
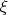
и х как множество в шестимерном пространстве - получится просто кратный интеграл по этому множеству. Так Вы избавитесь от двух интегралов, то есть запишите задачу одним интегралом. Правда, я не уверен, что такая запись задачу упростит- обычно делают наоборот: стараются понизить размерность, но на Ваш вопрос она дает ответ.