Добрый день. Как известно, реальный кепстр есть обратное преобразование Фурье от логарифма модуля прямого преобразования Фурье, т.е. rc(n)= ifft(log(abs(fft(x(n))))) , где x(n) -исходная числовая последовательность, а rc(n) её реальный кепстр.
Мною проводились исследования зависимости реального кепстра от длины последовательности x(n), которая представляет из себя белый гаусссовский шум. Далее представлены графики мат ожидания и дисперсии реального кепстра в двух случаях. В каждом из этих случаев было разное кол-во отсчетов БГШ , и каждый раз они дополнялись нулями до 2000 отсчетов
На этом рисунке x(n) - это 100 отсчетов БГШ и 1900 нулей
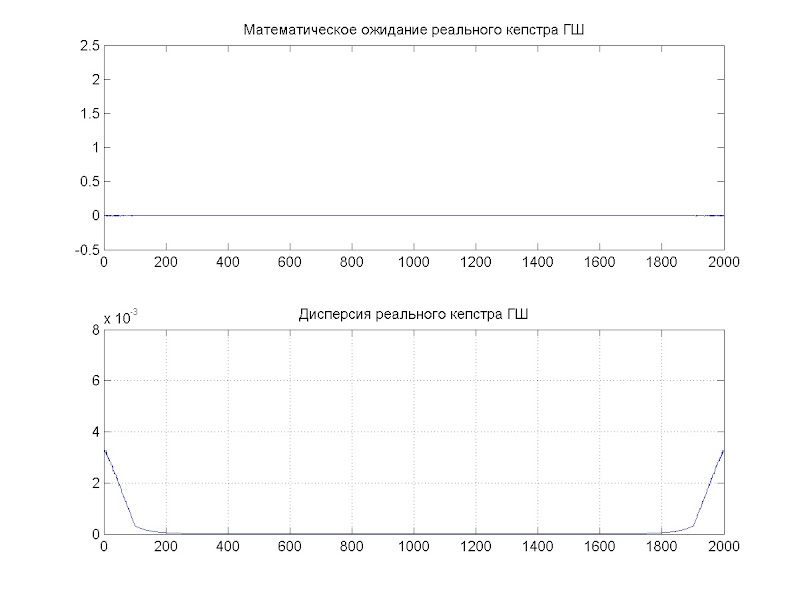
На этом рисунке x(n) - это 1000 отсчетов БГШ и 1000 нулей

Т.е. видно, что чем больше отсчетов ГШ мы возьмем, тем меньше дисперсия кепстра. Но при этом она как бы размазывается по всему интервалу.
Вопрос : Почему таким странным образом ведет себя дисперсия ? Ведь если рассматривать обычное преобразование Фурье, то там ситуация противоположная, т.е. чем больше отсчетов возьмем, тем больше будут значения спектра амплитуд