Уравнение

задаёт целую параболу, а на Вашем рисунке - только половина. И условия
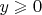
в задаче нету, так что границе

взяться неоткуда.
P.S. Вообще-то, свои задачи следует в своей теме обсуждать. Но, может быть,
wladimirdead на Ваши рисунки посмотрит, и ему придёт в голову идея свой рисунок сделать...