исследовать сходимость ряда по второму признаку.

[wolfpredator]

Добрый вечер всем.
Хочу проверить себя.
Дан ряд (2^n+1)\(5^n+1)
и сравнивать его предлагают с (2\5)^n
в итого мне получается надо взять предел от (10^n+5^n)\(10^n+2^n)?

[ИСН]

Дан самолёт. Хорошо. А сделать-то нужно что? Сфотографировать его? Покрасить в розовый цвет? Садиться и лететь бомбить Ливию?

[Whitaker]

Уважаемый wolfpredator! Вы наверное имели в виду такой ряд $\sum_{n=1}^{\infty}\frac{2^n+1}_{5^n+1}$ ?
Если такой, то данный ряд знакоположительный и ${\frac{2^n+1}_{5^n+1}}\sim {\frac{2^n}_{5^n}}=\left (\frac{2}_{5} \right )^n$ при $n\rightarrow\infty$ и ряд $\sum_{n=1}^{\infty}{\left (\frac{2}_{5} \right )^n$}$ сходится так как ${\frac{2}_{5}}<1$, то отсюда следует, что наш исходный ряд также сходится.

[wolfpredator]

Прошу прощение за несвязность вышеизложенного)
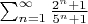
ряд действительно такой)
То что сходится я понимаю. Просто если это все расписывать, то я упираюсь в то что мне нужно взять предел ${\frac{10^n+5^n}{10^n+2^n}}$
Это я получаю исходя из второго признака сравнения рядов.
Тобишь $\lim\frac{A}{B}$, где $A=\sum_{n=1}^{\infty}\frac{2^n+1}{5^n+1}$, а $B=\sum_{n=1}^{\infty}\frac{2^n}{5^n}$
из этого получаю $\lim_{n=\infty}\frac{\sum_{n=1}^{\infty}\frac{2^n+1}{5^n+1}}{\sum_{n=1}^{\infty}\frac{2^n}{5^n}}$
но ведь такой предел бесконечен, или я ошибаюсь? Спасибо всем кто ответил.

[Joker_vD]

Это где вы такой признак откопали? Нет там никаких сумм, ищется предел отношения только членов:

$$\lim_{n\to\infty} \left(\frac{2^n+1}{5^n+1} \left/ \frac{2^n}{5^n} \right.\right) = \lim_{n\to\infty} \frac{10^n+5^n}{10^n+2^n} = \lim_{n\to\infty} \frac{1+\frac{1}{2^n}}{1+\frac{1}{5^n}}.$$

Ну и где здесь бесконечность?

[Whitaker]

Я не совсем понял чего вы хотите. Но могу сказать одно: этот предел конечен, а не бесконечен как вы утверждаете.
$\lim_{n\to\infty}\frac{10^n+5^n}{10^n+2^n}=\lim_{n\to\infty}\frac{\frac{10^n+5^n}_{10^n}}{\frac{10^n+2^n}_{10^n}}} = \lim_{n\to\infty}\frac{1+ \left (\frac{1}{2}\right )^n}{1+\left ( \frac{1}{5}\right )^n}=1$
P.S. Запись $\alpha_n\sim\beta_n$ при $n\to\infty$ означает, что $\lim_{n\to\infty\frac{\alpha_n}{\beta_n}=1}$
P.P.S. Скажите пожалуйста почему когда я пишу предел то запись $n\to\infty$ не стоит под $\lim$

[Tlalok]

(Оффтоп)

Whitaker
Вы правила форума читали?

[Whitaker]

Tlalok в сообщении #457601 писал(а):

(Оффтоп)

Whitaker
Вы правила форума читали?

Да, я читал. Извините пожалуйста, я что-нибудь нарушил?

[AKM]

Whitaker,

предупреждение за размещение решений простых учебных задач.
Правила этого раздела.

wolfpredator

Тема перемещена из "Помогите решить (М)" в карантин. В теме Что такое карантин, и что нужно делать, чтобы там оказаться также описано, как исправлять ситуацию.