Joker_vDПо-моему вы что-то путаете. При умножении матрицы размерности
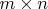
на матрицу

получается матрица размерности

. В моем случае: матрица(столбец) размерности

умножается на матрицу(строку со всеми единицами) размерности

, т.е. результатом будет матрица размерности

строки которой будут один в один повторять заданный столбец. Можете сами проверить в любой среде моделирования.)
Чувствуется, что должно быть красивое решение, осталось только найти правильную последовательность операций и правильных ее участников.. какие-то "константные матрицы", видимо..